“If you tell me that curiosity killed the cat, I say only the cat died nobly.”
– Arnold Edinborough
Intro
Sparse rewards make it hard for RL algorithms to learn. Relying on random exploration to stumble into a state with a reward is only feasible for trivial tasks. This paper proposes an intrinsic reward signal, or curiosity, to reward the agent to explore its environment in a tractable way. It introduces the Intrinsic Curiosity Module, or ICM to provide an additional reward $r^i_t$ along with the external reward $r^e_t$ with the policy optimizing $r_t = r^i_t + r^e_t$.
Intrinsic Curiosity Module
This is just matrix multiplication.
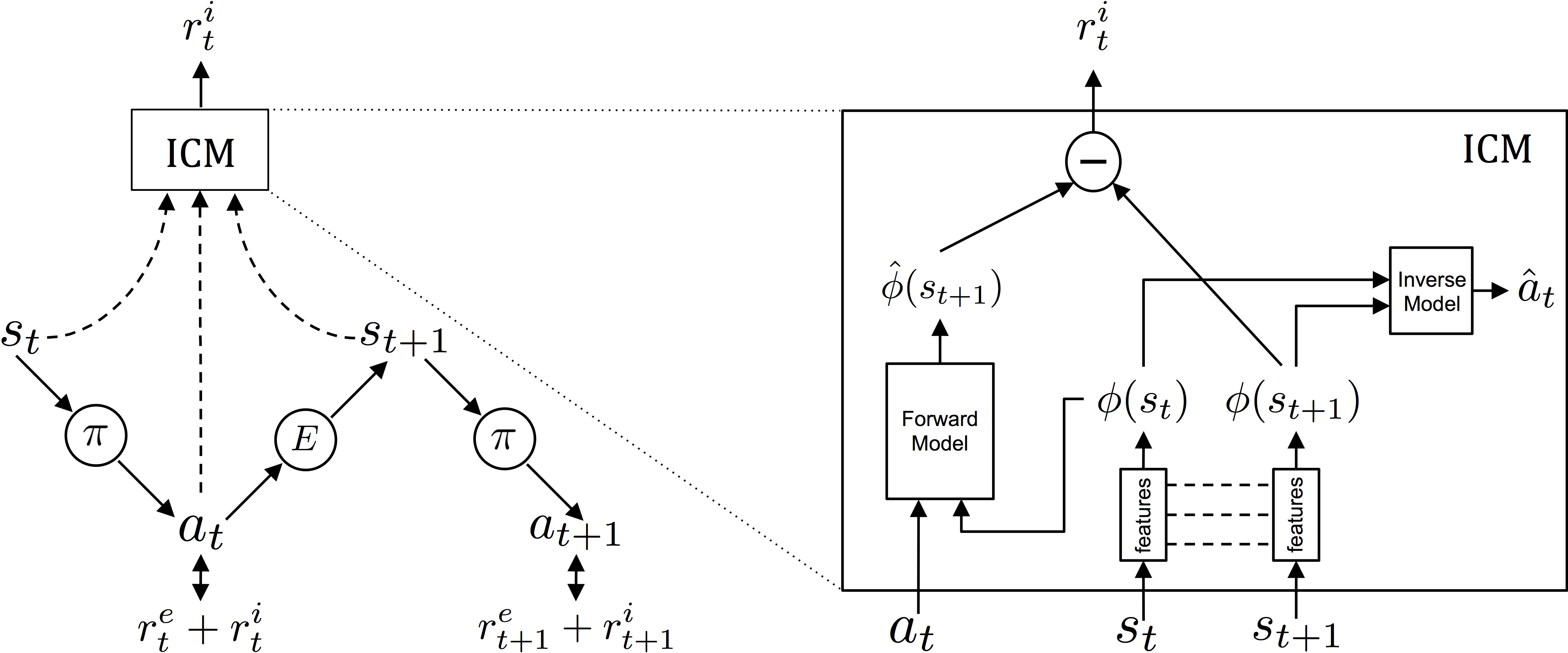
We use the ICM to output an intrinsic reward signal. It represents the curiosity, or how different the new state is. It takes in the previous state $s_t$, action $a_t$, and resulting state of the action $s_{t+1}$ and outputs $r^i_t$. How is it computed?
Consider a video game with pixels as its observation state. A naive way is to literally take the difference between new state and old state and the difference in pixels would represent how different the states are. However, consider leaves blowing or a fan spinning. These constantly stochastic phenomena would incorrectly give high curiosity to the agent. What we need is an encoding to project the raw observations into a feature space invariant to parts of the environment that the agent cannot affect. Let’s assume we have that first.
Predictor
How do we define curiosity? We can say it is how unfamiliar we are with the new state $s_{t+1}$. We use a neural network $F$ to approximate how familiar we are with the new state $s_{t+1}$. It will predict the new state encoding $\hat{\phi}(s_{t+1})$ given the old state encoding $\phi(s_t)$ and the action $a_t$.
\[F\big(\phi(s_t), a_t; \theta_F\big)\rightarrow\hat{\phi}(s_{t+1})\]We train this network by optimizing the distance between the predicted new state encoding and actual new state encoding.
\[L_F\big(\phi(s_t),\hat{\phi}(s_{t+1})\big) = \frac{1}{2}\left\| \hat{\phi}(s_{t+1}) - \phi(s_{t+1}) \right\|_2^2 \\ \underset{\theta_F}\min L_F\big(\phi(s_t),\hat{\phi}(s_{t+1})\big)\]Finally, the curiosity / intrinsic reward at time $t$ ($r^i_t$) is computed as the distance between the predicted new state encoding and actual new state encoding.
\[r^i_t = \frac{1}{2}\left\| \hat{\phi}(s_{t+1}) - \phi(s_{t+1}) \right\|_2^2\]So imagine a new state that we have not seen before. $F$ will give a bad prediction and the resulting distance between the predicted new state encoding and the actual new state encoding will be high. On the other hand, if the new state has been seen before, the forward model will give a good prediction of the new state encoding and the distance will be low.
This assumes we have a good encoding of the environment, which is invariant to parts of the environment that do not affect the agent or task. We learn this by using the encoding as part of a NN to predict an action given the old and new state.
Encoding
To do this, we will first use a neural network to learn an encoding $\phi(s_t)$ of the observation space. The encoding should only take into account parts of the environment the agent can change with its own actions or will affect the agent in some way. How do we learn this encoding?
We train a neural network, $I$, that has two sub-modules, $\phi$ and $g$. The first sub-module encodes $s_t$ into an encoding $\phi(s_t)$. The second sub-module takes current and next state encodings to predict the action that caused the transition between the states.
\[I(s_t, s_{t+1}; \theta_I) = g\big(\phi(s_t), \phi(s_{t+1})\big)\\ I(s_t, s_{t+1}; \theta_I) \rightarrow\hat{a}_t\]We optimize it using the distance between the predicted action and actual action. The distance is computed using a soft max over the action distributions for discrete actions.
\[\underset{\theta_I}\min L_I(\hat{a}_t, a_t)\]By training this proxy prediction task, it will give us encodings that represent parts of the environment the agent can affect through its actions. This is because in order to predict an action \((\hat{a}_t)\) given only the old and current state \((s_t, s_{t+1})\), the encodings are incentivized to encode environmental features that are influenced by the agent.
Results
The ICM agent is able to learn quicker and is able to explore more efficiently than A3C and pixel based curiosity agents.This translates to higher performance than the baselines. One interesting experiment the authors show is playing Mario with only curiosity rewards. The agent learns to kill enemies without any external reward. The agent is incentivized to kill enemies so it can continue exploration, whereas if it dies from the enemy it will have a lower curiosity reward.